Skip to content

2. Lattice

The aim of the current section is to help us gain familiarity with the lattice model of KITE. Thus, we begin by constructing a periodic pb.Lattice using Pybinding and calculating its band structure using pb.Solver (also from Pybinding). In the following sections, we will learn how to use KITEx to significantly scale up the simulations and introduce modifications to the lattice model.

For efficiency, the default options of KITE's core code (KITEx) assume that the lattice model has a certain degree of interconnectivity or hopping range. Specifically, the default is that the tight-binding Hamiltonian has non-zero matrix elements between orbitals that belong to unit cells that are separated by at most 2 lattice spacings along a given direction (for example, in a simple single-orbital 1D chain this would allow defining models with up to second-nearest neighbors). To relax this constraint and thus be able to simulate more complex lattice models, users must adjust the NGHOSTS parameter in kite/Src/Generic.hpp and recompile KITEx, otherwise an error message is output and the KITE program exits.

Info

If you are familiar with Pybinding, you can go directly to the next tutorial page.

Note

The python script that generates KITE's input file requires a few packages that can be included with the following aliases

import kite
import pybinding as pb
import numpy as np
import matplotlib.pyplot as plt

Constructing a pb.Lattice

The pb.Lattice class from Pybinding carries the information about the TB model. This includes:

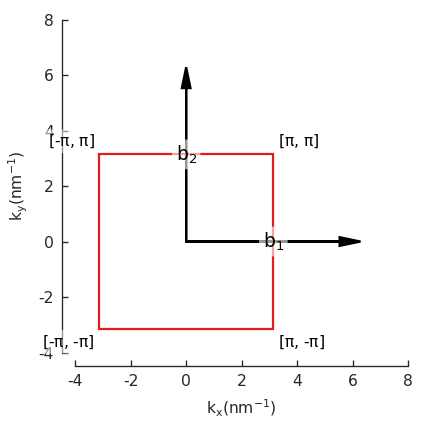
Pybinding also provides additional functionalities based on the above real-space information. For example, it can prove the reciprocal vectors and the Brillouin zone.

Defining the unit cell

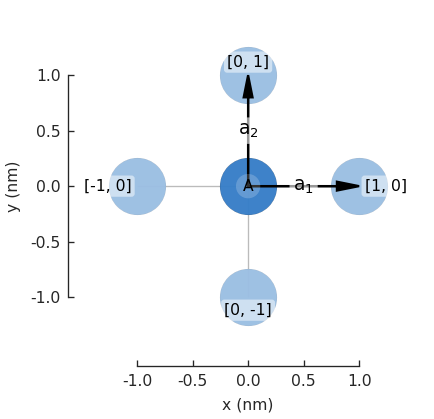
As a simple example, let us construct a square lattice with a single orbital per unit cell. The following syntax can be used to define the primitive lattice vectors:

1
2
3
4
a1 = np.array([1, 0]) # [nm] defines the first lattice vector
a2 = np.array([0, 1]) # [nm] defines the second lattice vector

lat = pb.Lattice(a1=a1, a2=a2) # defines a lattice object

Adding lattice sites

We can then add the desired lattice sites/orbitals inside the unit cell (the same syntax can be used to add different orbitals in a given position or more sites in different sublattices):

1
2
3
4
5
6
onsite = 0 # onsite potential
lat.add_sublattices(
    # generates a lattice site (sublattice) with a tuple
    # (name, position, and onsite potential)
    ('A', [0, 0], onsite)
)

Adding hoppings

By default, the main unit cell has the index [n1,n2] = [0, 0]. The hoppings between neighboring sites can be added with the simple syntax:

1
2
3
4
5
6
lat.add_hoppings(
    # generated a hopping between lattice sites with a tuple
    # (relative unit cell index, site from, site to, hopping energy)
    ([1, 0], 'A', 'A', - 1 ),
    ([0, 1], 'A', 'A', - 1 )
)

Here, the relative indices n1,n2 represent the number of integer steps - in units of the primitive lattice vectors - needed to reach a neighboring cell starting from the origin.

If the lattice has more than one sublattice, the hoppings can connect sites in the same unit cell.

Note

When adding the hopping (n, m) between sites n and m, the conjugate hopping term (m, n) is added automatically. Pybinding does not allow the user to add them manually.

Visualization

Now we can plot the pb.lattice and visualize the Brillouin zone:

1
2
3
4
5
lat.plot()
plt.show()

lat.plot_brillouin_zone()
plt.show()
The visualization of the lattice and its Brillouin zone.

Examples

For a crystal with two atoms per unit cell, look in the Examples section. For other examples and pre-defined lattices, consult the Pybinding documentation.

Using Pybinding's solver

Pybinding has built-in solvers for

  • LAPACK (exact diagonalization)
  • ARPACK (targeted diagonalization of sparse matrices)

To use any of these solvers, we need to first construct a model.

Building a pb.Model

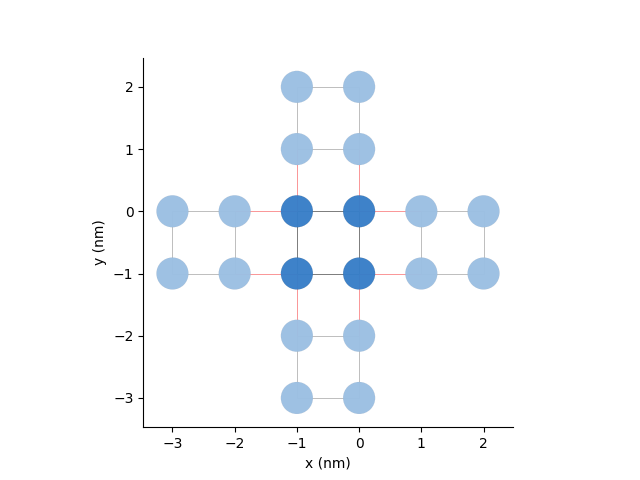
The pb.Model class contains all the information of the structure we want to use in our calculation. This structure can be significantly larger than the unit cell (stored in the pb.Lattice class). It can also have specific geometries and other possible modifications of the original lattice. Here, we will double the unit cell in both directions in the pb.Model and add periodic boundary conditions: 

1
2
3
4
5
model = pb.Model(
    lat,  # pb.Lattice, uses the previously defined unit-cell
    pb.primitive(2, 2),  # doubles the unit-cell in both directions
    pb.translational_symmetry(a1=2, a2=2)  # periodic boundary conditions with period '2'
)
We can visualise this pb.Model with 
1
2
model.plot()
plt.show()

The visualization of the model.

Defining a pb.Solver

The pb.Solver class takes a pb.Model class as input and prepares the system to perform a numerical calculation. We will use the LAPACK solver: 

1
2
3
solver = pb.solver.lapack(
    model  # pb.Model, use the previously defined system
)

Band structure calculation

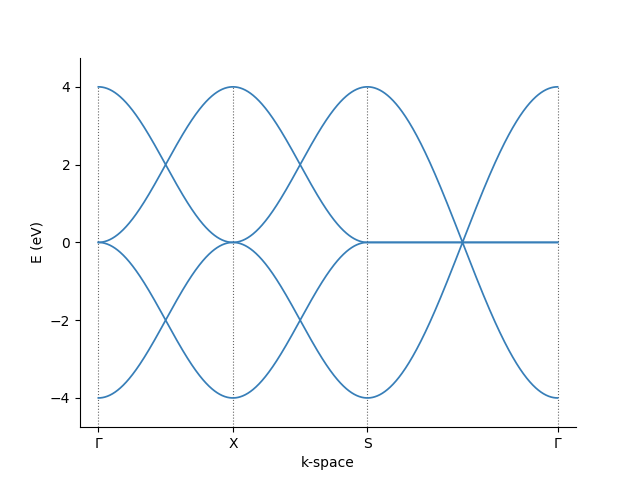
As an example, the band structure is calculated using the pb.Solver defined above.

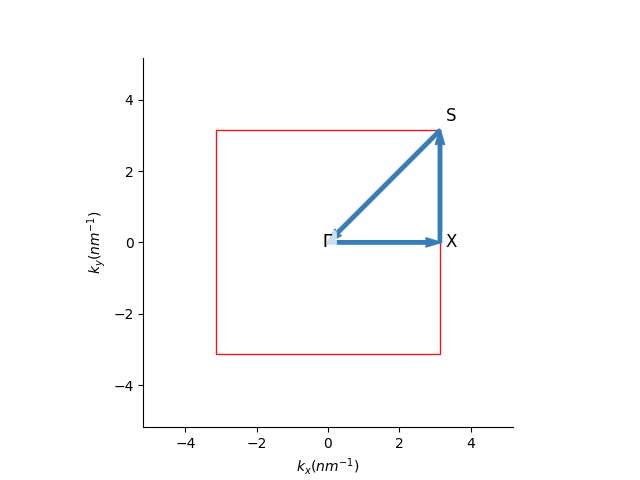
First, for a two-dimensional plot, we define a path in the reciprocal space that connects the high symmetry points. Using the pb.Lattice built-in method, the high-symmetry points for the corners of a path can be found easily: 

1
2
3
4
bz = lat.brillouin_zone()
gamma = np.array([0, 0]) 
x = (bz[1] + bz[2]) / 2
s = bz[2]

We can then pass these corners to the pb.Solver and visualize the result 

1
2
3
4
5
6
7
bands = solver.calc_bands(gamma, x, s, gamma, step=0.01)
bands.plot(point_labels=[r"$\Gamma$", "X", "S", r"$\Gamma$"])
plt.show()

lat.plot_brillouin_zone(decorate=False)
bands.k_path.plot(point_labels=[r"$\Gamma$", "X", "S", r"$\Gamma$"])
plt.show()

The visualization of the band structure and its path in the reciprocal space.

For more info about Pybinding's capabilities, look at its tutorial or API guide.

Summary of the code from this section

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import kite
import pybinding as pb
import numpy as np
import matplotlib.pyplot as plt

a1 = np.array([1, 0]) # [nm] define the first lattice vector
a2 = np.array([0, 1]) # [nm] define the second lattice vector

lat = pb.Lattice(a1=a1, a2=a2) # define a lattice object


onsite = 0 # onsite potential
lat.add_sublattices(
    # make a lattice site (sublattice) with a tuple
    # (name, position, and onsite potential)
    ('A', [0, 0], onsite)
)

lat.add_hoppings(
    # make an hopping between lattice site with a tuple
    # (relative unit cell index, site from, site to, hopping energy)
([1, 0], 'A', 'A', - 1 ),
([0, 1], 'A', 'A', - 1 )
)

model = pb.Model(
    lat,  # pb.Lattice, use the previously defined unit-cell
    pb.primitive(2, 2),  # double the unit-cell in both directions
    pb.translational_symmetry(a1=2, a2=2)  # periodic boundary conditions with period '2'
)

solver = pb.solver.lapack(
    model  # pb.Model, use the previously defined system
)

bz = lat.brillouin_zone()
gamma = np.array([0, 0]) 
x = (bz[1] + bz[2]) / 2
s = bz[2]

bands = solver.calc_bands(gamma, x, s, gamma, step=0.01)
bands.plot(point_labels=[r"$\Gamma$", "X", "S", r"$\Gamma$"])
plt.show()

lat.plot_brillouin_zone(decorate=False)
bands.k_path.plot(point_labels=[r"$\Gamma$", "X", "S", r"$\Gamma$"])
plt.show()